


Linear Regression is the simplest form of predictive modeling. It assumes a straight-line relationship between two variables. For example:
More study hours → Higher exam scores
This relationship can be modeled as
y=mx+c
Where:
m: Slope (how fast y changes when x changes)
c: Intercept (the starting point of the line)
Given some data, Linear Regression helps us find m and c automatically.
1)
First, we need to calculate the average of a list of numbers.
(defun mean (lst)
(/ (reduce #'+ lst) (length lst)))
2)
Variance measures how spread out a list of numbers is.
(defun variance (lst)
(let ((m (mean lst)))
(mean (mapcar (lambda (x) (expt (- x m) 2)) lst))))
3)
Covariance tells us how two variables change together.
(defun covariance (x y)
(let* ((mean-x (mean x))
(mean-y (mean y))
(n (length x))
(sum 0))
(dotimes (i n)
(incf sum (* (- (nth i x) mean-x)
(- (nth i y) mean-y))))
(/ sum n)))
4)
This is where we calculate our model’s intercept and slope (our c and c).
(defun linear-regression-coeffs (x y)
(let ((b1 (/ (covariance x y) (variance x))))
(let ((b0 (- (mean y) (* b1 (mean x)))))
(list b0 b1))))
5)
Finally, given x, this function predicts y using our model.
(defun predict (model x)
(+ (first model) (* (second model) x)))
6)
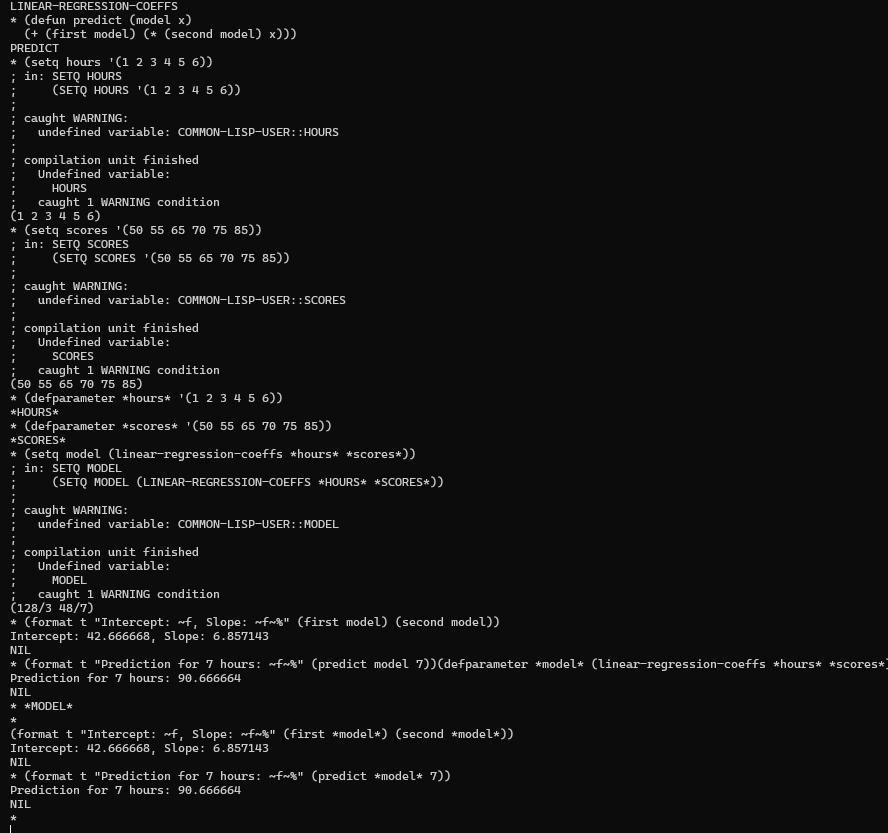
(defparameter *hours* '(1 2 3 4 5 6))
(defparameter *scores* '(50 55 65 70 75 85))
(defparameter *model* (linear-regression-coeffs *hours* *scores*))
(format t "Intercept: ~f, Slope: ~f~%" (first *model*) (second *model*))
(format t "Prediction for 7 hours: ~f~%" (predict *model* 7))
7) Output
Intercept: 42.666668, Slope: 6.857143
Prediction for 7 hours: 90.666668
Intercept: 42.66 → Predicted score if study hours were zero.
Slope: 6.85 → Each extra hour of study increases the score by ~6.85 points.
Prediction for 7 hours: Expected score ~90.66